enDAQ Custom Analysis¶
Introduction¶
This notebook and accompanying webinar was developed and released by the enDAQ team. This is the fifth “chapter” of our series on Python for Mechanical Engineers:
Introduction of the enDAQ Library
There are lots of examples in this!
More Examples! (Today’s Webinar)
Frequency Analysis (FFTs and PSDs)
Simple Shock Response Spectrums
Peak Analysis
Preview
endaq.batch
To sign up for future webinars and watch previous ones, visit our webinars page.
Installation¶
Available on PyPi via: > pip install endaq
For the most recent features that are still under development, you can also use pip to install endaq directly from GitHub: > pip install git+https://github.com/MideTechnology/endaq-python.git@development
[ ]:
!pip install -q endaq
!pip install -q kaleido #this is for rendering images with plotly
exit() #needed in Colab because they pre-load some libraries, wouldn't be neccessary if running locally
|████████████████████████████████| 71 kB 3.0 MB/s
|████████████████████████████████| 11.3 MB 13.0 MB/s
|████████████████████████████████| 62 kB 749 kB/s
|████████████████████████████████| 38.1 MB 1.3 MB/s
|████████████████████████████████| 93 kB 1.0 MB/s
|████████████████████████████████| 83 kB 1.0 MB/s
|████████████████████████████████| 25.3 MB 51.8 MB/s
ERROR: pip's dependency resolver does not currently take into account all the packages that are installed. This behaviour is the source of the following dependency conflicts.
google-colab 1.0.0 requires pandas~=1.1.0; python_version >= "3.0", but you have pandas 1.3.4 which is incompatible.
google-colab 1.0.0 requires requests~=2.23.0, but you have requests 2.26.0 which is incompatible.
datascience 0.10.6 requires folium==0.2.1, but you have folium 0.8.3 which is incompatible.
albumentations 0.1.12 requires imgaug<0.2.7,>=0.2.5, but you have imgaug 0.2.9 which is incompatible.
|████████████████████████████████| 79.9 MB 1.2 MB/s
[ ]:
import endaq
endaq.plot.utilities.set_theme(theme='endaq')
import plotly.express as px
import plotly.graph_objects as go
import plotly.io as pio; pio.renderers.default = "iframe"
import pandas as pd
import numpy as np
import scipy
PSDs & FFTs¶
Simple Sine Wave¶
[ ]:
time = np.linspace(0,2,200,endpoint=False)
sine_waves = pd.DataFrame(index=time)
sine_waves['0.8g @ 2 Hz'] = 0.8*np.sin(2*np.pi*2 * time)
sine_waves['1g @ 3 Hz'] = np.sin(2*np.pi*3 * time)
sine_waves['0.6g @ 5 Hz'] = 0.6*np.sin(2*np.pi*5 * time)
sine_waves['0.5g @ 4 & 6 Hz'] = 0.5*np.sin(2*np.pi*4 * time) + 0.5*np.sin(2*np.pi*6 * time)
sine_waves['0.3g @ 7 Hz'] = 0.3*np.sin(2*np.pi*7 * time)
sine_waves
| 0.8g @ 2 Hz | 1g @ 3 Hz | 0.6g @ 5 Hz | 0.5g @ 4 & 6 Hz | 0.3g @ 7 Hz | |
|---|---|---|---|---|---|
| 0.00 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| 0.01 | 0.100267 | 0.187381 | 0.185410 | 0.308407 | 0.127734 |
| 0.02 | 0.198952 | 0.368125 | 0.352671 | 0.583150 | 0.231154 |
| 0.03 | 0.294500 | 0.535827 | 0.485410 | 0.794687 | 0.290575 |
| 0.04 | 0.385403 | 0.684547 | 0.570634 | 0.921177 | 0.294686 |
| ... | ... | ... | ... | ... | ... |
| 1.95 | -0.470228 | -0.809017 | -0.600000 | -0.951057 | -0.242705 |
| 1.96 | -0.385403 | -0.684547 | -0.570634 | -0.921177 | -0.294686 |
| 1.97 | -0.294500 | -0.535827 | -0.485410 | -0.794687 | -0.290575 |
| 1.98 | -0.198952 | -0.368125 | -0.352671 | -0.583150 | -0.231154 |
| 1.99 | -0.100267 | -0.187381 | -0.185410 | -0.308407 | -0.127734 |
200 rows × 5 columns
[ ]:
fig = px.line(sine_waves)
fig.update_layout(
title_text='Comparison of Fabricated Sine Waves',
yaxis_title_text='Acceleration (g)',
xaxis_title_text='Time (s)',
legend_title_text=''
)
Now to compute the PSD on this using endaq.calc.psd.welch(), see docs
[ ]:
psd = endaq.calc.psd.welch(sine_waves, bin_width=0.5)
[ ]:
fig = px.line(psd)
fig.update_layout(
title_text='Comparison of the PSD of Two Fabricated Sine Waves',
yaxis_title_text='Acceleration (g^2/Hz)',
xaxis_title_text='Frequency (Hz)',
xaxis_type='log',
legend_title_text=''
)
PSDs are the more appropriate way to analyze vibration data for a number of reasons (see blog) but we typically see people want to see the FFT because it’s units are easier to intuitively understand.
In my experience the best way to do this is to compute a PSD using our function with a few modifications: - Use scaling as parseval which means it is g^2 instead of g^2/Hz - Use a boxcar window so in effect there is no windowing - Define a very fine bin width - Set the overlap between FFTs to 0 (not necessary if the bin width is small enough) - Scale from g^2 as RMS to g-peak via **2 * (2**0.5)
[ ]:
fft = endaq.calc.psd.welch(
sine_waves,
scaling='parseval',
window='boxcar',
noverlap=0,
bin_width=0.1,
)
fft = fft**0.5 * (2**0.5) #scale from g^2 as RMS to g-peak
fig = px.line(fft)
fig.update_layout(
title_text='Comparison of the FFT (from PSD) of Two Fabricated Sine Waves',
yaxis_title_text='Acceleration (g)',
xaxis_title_text='Frequency (Hz)',
xaxis_type='log',
legend_title_text='',
template='endaq_light'
)
/usr/local/lib/python3.7/dist-packages/scipy/signal/spectral.py:1966: UserWarning:
nperseg = 1000 is greater than input length = 200, using nperseg = 200
Real Sine Wave¶
Let’s load a IDE file with get_doc docs.
[ ]:
doc = endaq.ide.get_doc('https://info.endaq.com/hubfs/100Hz_shake_cal.ide')
endaq.ide.get_channel_table(doc)
| channel | name | type | units | start | end | duration | samples | rate | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 8.0 | X (100g) | Acceleration | g | 00:00.0218 | 00:25.0532 | 00:25.0314 | 126575 | 5000.07 Hz |
| 1 | 8.1 | Y (100g) | Acceleration | g | 00:00.0218 | 00:25.0532 | 00:25.0314 | 126575 | 5000.07 Hz |
| 2 | 8.2 | Z (100g) | Acceleration | g | 00:00.0218 | 00:25.0532 | 00:25.0314 | 126575 | 5000.07 Hz |
| 3 | 80.0 | X (40g) | Acceleration | g | 00:00.0218 | 00:25.0547 | 00:25.0328 | 100934 | 3985.00 Hz |
| 4 | 80.1 | Y (40g) | Acceleration | g | 00:00.0218 | 00:25.0547 | 00:25.0328 | 100934 | 3985.00 Hz |
| 5 | 80.2 | Z (40g) | Acceleration | g | 00:00.0218 | 00:25.0547 | 00:25.0328 | 100934 | 3985.00 Hz |
| 6 | 36.0 | Pressure/Temperature:00 | Pressure | Pa | 00:00.0217 | 00:25.0702 | 00:25.0485 | 27 | 1.06 Hz |
| 7 | 36.1 | Pressure/Temperature:01 | Temperature | °C | 00:00.0217 | 00:25.0702 | 00:25.0485 | 27 | 1.06 Hz |
| 8 | 70.0 | X | Quaternion | q | 00:00.0284 | 00:24.0682 | 00:24.0397 | 2424 | 99.35 Hz |
| 9 | 70.1 | Y | Quaternion | q | 00:00.0284 | 00:24.0682 | 00:24.0397 | 2424 | 99.35 Hz |
| 10 | 70.2 | Z | Quaternion | q | 00:00.0284 | 00:24.0682 | 00:24.0397 | 2424 | 99.35 Hz |
| 11 | 70.3 | W | Quaternion | q | 00:00.0284 | 00:24.0682 | 00:24.0397 | 2424 | 99.35 Hz |
| 12 | 59.0 | Control Pad Pressure | Pressure | Pa | 00:00.0251 | 00:25.0399 | 00:25.0148 | 252 | 10.02 Hz |
| 13 | 59.1 | Control Pad Temperature | Temperature | °C | 00:00.0251 | 00:25.0399 | 00:25.0148 | 252 | 10.02 Hz |
| 14 | 59.2 | Relative Humidity | Relative Humidity | RH | 00:00.0251 | 00:25.0399 | 00:25.0148 | 252 | 10.02 Hz |
| 15 | 76.0 | Lux | Light | Ill | 00:00.0000 | 00:25.0278 | 00:25.0278 | 100 | 3.96 Hz |
| 16 | 76.1 | UV | Light | Index | 00:00.0000 | 00:25.0278 | 00:25.0278 | 100 | 3.96 Hz |
Now get the actual data out of one channel with to_pandas() docs.
Then generate a plot with rolling_min_max_envelope() (docs) that will instead of plotting all data points make a shaded plot which will look identical to plotting all points but be more responsive and faster (not entirely necessary on this dataset, but becomes so with larger ones).
[ ]:
accel = endaq.ide.to_pandas(doc.channels[80], time_mode='seconds')
accel = accel-accel.median() #remove DC offset
endaq.plot.rolling_min_max_envelope(
accel,
plot_as_bars=True,
desired_num_points=1000,
opacity=0.7
)
Here we’ll plot the raw data around the peak event with around_peak() docs.
[ ]:
endaq.plot.around_peak(accel, num=500)
[ ]:
fft = endaq.calc.psd.welch(
accel[4.5:9.5], #just do it in time of first dwell
scaling='parseval',
window='boxcar',
noverlap=0,
bin_width=0.5,
)
fft = fft**0.5 * (2**0.5) #scale from g^2 as RMS to g-peak
fig = px.line(fft[:500])
fig.update_layout(
title_text='FFT (from PSD) of Real World 10.3g Sine Wave',
yaxis_title_text='Acceleration (g)',
xaxis_title_text='Frequency (Hz)',
legend_title_text='',
)
Comparing FFT Options¶
FFT Option Overview¶
There are a lot of different ways to compute a FFT in Python. I’ve been using Welch’s method so far but I want to compare that to some other more “direct” methods. So let’s compare them! First let’s conveniently wrap our manipulation of Welch’s method PSD into a FFT inside a function.
[ ]:
def welch_fft(df, bin_width=0.5):
fft = endaq.calc.psd.welch(df, bin_width=bin_width, scaling='parseval', window='boxcar', noverlap=0)
return fft**0.5 * (2**0.5) #scale from g^2 as RMS to g-peak
Now let’s wrap something around Numpy’s FFT functions for a real discrete Fourier transform.
Notice here we actually have phase information! So we’ll return that too.
[ ]:
def numpy_fft(df):
"""
Using Numpy's rfft functions compute a discrete Fourier Transform
"""
freq = np.fft.rfftfreq(len(df), d=endaq.calc.utils.sample_spacing(df))
df_fft = pd.DataFrame(
np.fft.rfft(df.to_numpy(), axis=0),
index=pd.Series(freq, name="frequency (Hz)"),
columns=df.columns
)
df_mag = df_fft.apply(np.abs, raw=True) / len(df_fft)
df_phase = df_fft.apply(np.angle, raw=True)
return df_mag, df_phase
Now we will use the FFTW algorithm which is available in the pyFFTW library under a GPL license (which makes it potentially difficult for us to use because we use the more premissive MIT license).
First let’s download it.
[ ]:
!pip install -q pyfftw
|████████████████████████████████| 2.6 MB 5.3 MB/s
Now let’s use it in a function which allows for a drop-in replacement to the Numpy code. This algorithm is generally regarded as the fatest for computing discrete Fourier transforms - so we’ll put it to the test!
[ ]:
import pyfftw
def fftw_fft(df):
"""
Using the FFTW algorithm, compute a discrete Fourier Transform
"""
freq = pyfftw.interfaces.numpy_fft.rfftfreq(len(df), d=endaq.calc.utils.sample_spacing(df))
df_fft = pd.DataFrame(
pyfftw.interfaces.numpy_fft.rfft(df.to_numpy(), axis=0),
index=pd.Series(freq, name="frequency (Hz)"),
columns=df.columns
)
df_mag = df_fft.apply(np.abs, raw=True) / len(df_fft)
df_phase = df_fft.apply(np.angle, raw=True)
return df_mag, df_phase
Now let’s see a FFT result with this library. Note though this will be relatively large to plot…
[ ]:
fft, phase = fftw_fft(accel[4.5:9.5])
fig = px.line(fft[80:120])
fig.update_layout(
title_text='FFT using FFTW of Real World 10.3g Sine Wave',
yaxis_title_text='Acceleration (g)',
xaxis_title_text='Frequency (Hz)',
legend_title_text='',
)
Remember one of the benefits of the DFT is to get phase. Although not particularly useful for this dataset let’s plot it, notice the shift for the Z axis at the drive frequency.
[ ]:
fig = px.line(phase[80:120])
fig.update_layout(
title_text='Phase using FFTW of Real World 10.3g Sine Wave',
yaxis_title_text='Phase Angle (radians)',
xaxis_title_text='Frequency (Hz)',
legend_title_text='',
)
FFT Option Comparison¶
Now let’s do the fun part to compare the three approaches! First let’s make a sine wave with a bit over 1M points.
[ ]:
time = np.linspace(0,200,2**20,endpoint=False)
sine_waves = pd.DataFrame(index=time)
sine_waves['10g @ 100 Hz'] = 10*np.sin(2*np.pi*100 * time)
sine_waves['8g @ 99 Hz'] = 8*np.sin(2*np.pi*99 * time)
sine_waves['6g @ 100.25 Hz'] = 6*np.sin(2*np.pi*100.25 * time)
[ ]:
fig = px.line(sine_waves[:0.01])
fig.update_layout(
title_text='Comparison of Fabricated Sine Waves',
yaxis_title_text='Acceleration (g)',
xaxis_title_text='Time (s)',
legend_title_text=''
)
[ ]:
from time import process_time
import timeit
pyfftw.forget_wisdom() #FFTW will be faster on subsequent runs
lengths = [2**14, 16411, 2**17, 131101, 2**20, 1000003]
ffts = pd.DataFrame()
times = pd.DataFrame()
def melt_fft(fft,name,L):
fft = fft.reset_index().melt(id_vars='frequency (Hz)')
fft['Algo'] = name
fft['Length'] = L
return fft
def time_fft(func):
return np.array(timeit.repeat(func, number=1, repeat=10)).mean()
def time_pyfftw(x, threads=1):
pyfftw.forget_wisdom()
rfft = pyfftw.builders.rfft(x, threads=threads, auto_align_input=True)
rfft()
return np.array(timeit.repeat(lambda: rfft(), number=1, repeat=10)).mean()
for L in lengths:
x = sine_waves.iloc[:L, 0].to_numpy()
t1 = process_time()
wfft_bin = welch_fft(sine_waves.iloc[:L], bin_width=0.5)
t2 = process_time()
wfft = welch_fft(sine_waves.iloc[:L], bin_width=1/(L*endaq.calc.utils.sample_spacing(sine_waves)))
t3 = process_time()
nfft, phase = numpy_fft(sine_waves.iloc[:L])
t4 = process_time()
fftw, phase = fftw_fft(sine_waves.iloc[:L])
t5 = process_time()
times_t = pd.DataFrame(
{'Welch w/ 0.5 Hz Bin':t2-t1,
'Welch': t3-t2,
'Numpy':t4-t3,
'FFTW':t5-t4,
'Numpy - No OH': time_fft(lambda: np.fft.rfft(x)),
'FFTW - No OH': time_pyfftw(x, threads=1)
},
index=pd.Series([L],name='Length')
)
times = pd.concat([times,times_t.reset_index().melt(id_vars='Length')])
wfft_bin = melt_fft(wfft_bin.copy(),'Welch w/ 0.5 Hz Bin',L)
wfft = melt_fft(wfft.copy(),'Welch',L)
nfft = melt_fft(nfft.copy(),'Numpy',L)
fftw = melt_fft(fftw.copy(),'FFTW',L)
ffts = pd.concat([ffts,wfft_bin,wfft,nfft,fftw])
[ ]:
times['str_len'] = times['Length'].astype('str')
fig = px.bar(
times,
x='str_len',
y='value',
color='variable',
log_y=True,
barmode='group',
labels={'value':'Computation Time (s)','str_len':'Array Length','variable':''}
)
fig.show()
[ ]:
fig = px.scatter(
times,
x='str_len',
y='value',
color='variable',
log_y=True,
log_x=True,
labels={'value':'Computation Time (s)','str_len':'Array Length','variable':''}
)
fig.show()
So what does this mean!? FFTW is the fastest as expected, but only if we first structure the data in a more efficient way. But typically you will not have the data structured in this “optimal” way for FFTW which means the time it takes to restucture it is real.
Long story short for this audience, using Welch’s method is fastest!
[ ]:
fig = px.line(
ffts[(ffts['frequency (Hz)']>95) & (ffts['frequency (Hz)']<105)],
x='frequency (Hz)',
y='value',
color='Algo',
facet_col='Length',
facet_row='variable',
title='FFTs: Acceleration (g) vs Frequency (Hz)',
labels={'value':'','frequency (Hz)':''}
)
fig.for_each_annotation(lambda a: a.update(text=a.text.split("=")[-1]))
fig.update_layout(width=1200,height=1000)
fig.show()
[ ]:
fig.write_html('FFT-compare.html',include_plotlyjs='cdn')
When comparing the actual FFT results we notice that Welch’s with a fixed frequency bin width gives us identical results regardless of the time duration we use - and these are the “right” or at least expected result.
Random Vibration (NAVMAT PSD)¶
Let’s look at the NAVMAT PSD which is as follows: 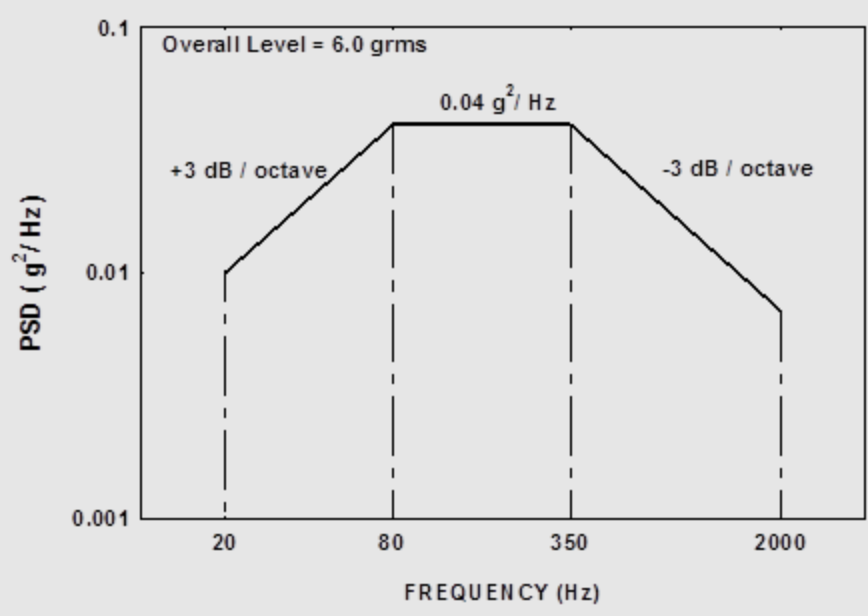
[ ]:
navmat = pd.read_csv('https://info.endaq.com/hubfs/navmat-p-9492.csv',delimiter='\t',header=None,index_col=0,names=['Random'])
navmat.index.name='Time (s)'
navmat['Add 2g @ 100 Hz'] = navmat.Random + 2*np.sin(2*np.pi*100 * navmat.index)
navmat['Add 2g @ 200 Hz'] = navmat.Random + 2*np.sin(2*np.pi*200 * navmat.index)
navmat['Add 2g @ 400 Hz'] = navmat.Random + 2*np.sin(2*np.pi*400 * navmat.index)
navmat
| Random | Add 2g @ 100 Hz | Add 2g @ 200 Hz | Add 2g @ 400 Hz | |
|---|---|---|---|---|
| Time (s) | ||||
| 0.000000 | -8.698490e-07 | -8.698490e-07 | -8.698490e-07 | -8.698490e-07 |
| 0.000038 | 8.459350e-07 | 4.793334e-02 | 9.583830e-02 | 1.914556e-01 |
| 0.000076 | 1.871620e-06 | 9.583932e-02 | 1.914566e-01 | 3.811528e-01 |
| 0.000114 | 3.444110e-06 | 1.436908e-01 | 2.866355e-01 | 5.673498e-01 |
| 0.000153 | 6.051080e-06 | 1.914608e-01 | 3.811570e-01 | 7.483369e-01 |
| ... | ... | ... | ... | ... |
| 9.999847 | 3.435810e-02 | -1.571110e-01 | -3.468213e-01 | -7.140265e-01 |
| 9.999886 | 3.562460e-02 | -1.080109e-01 | -2.509046e-01 | -5.315224e-01 |
| 9.999924 | 1.458970e-02 | -8.125498e-02 | -1.768794e-01 | -3.665897e-01 |
| 9.999962 | 1.604150e-02 | -3.183180e-02 | -7.967766e-02 | -1.751775e-01 |
| 10.000000 | -2.424250e-04 | -2.424250e-04 | -2.424250e-04 | -2.424250e-04 |
262144 rows × 4 columns
[ ]:
endaq.plot.rolling_min_max_envelope(navmat, plot_as_bars=True, desired_num_points=500, opacity=0.8)
[ ]:
endaq.plot.around_peak(navmat, num=1000)
FFTs¶
[ ]:
fft = welch_fft(navmat, bin_width=1)
fig = px.line(fft[20:2000])
fig.update_layout(
title_text='NAVMAT P-9492 FFT (1 Hz Bin Width)',
yaxis_title_text='Acceleration (g)',
xaxis_title_text='Frequency (Hz)',
xaxis_type='log',
yaxis_type='log',
legend_title_text=''
)
Now let’s demonstrate the trouble with FFTs by varying the length of time we’ll use and the bin width/resolution in the FFT.
[ ]:
bins = ['1/T', 1, 10]
times = [1.0, 10]
ffts = pd.DataFrame()
for bin in bins:
for time in times:
bin_t = bin
if bin=='1/T':
bin_t = 1/time
fft = welch_fft(navmat[:time], bin_width=bin_t)
fft = fft[20:2000].reset_index().melt(id_vars='frequency (Hz)')
fft['Time'] = time
fft['Bin Width'] = bin
ffts = pd.concat([ffts,fft])
ffts
| frequency (Hz) | variable | value | Time | Bin Width | |
|---|---|---|---|---|---|
| 0 | 20.000229 | Random | 0.288549 | 1.0 | 1/T |
| 1 | 21.000240 | Random | 0.169284 | 1.0 | 1/T |
| 2 | 22.000252 | Random | 0.099324 | 1.0 | 1/T |
| 3 | 23.000263 | Random | 0.101153 | 1.0 | 1/T |
| 4 | 24.000275 | Random | 0.100844 | 1.0 | 1/T |
| ... | ... | ... | ... | ... | ... |
| 787 | 1950.319916 | Add 2g @ 400 Hz | 0.388329 | 10.0 | 10 |
| 788 | 1960.321557 | Add 2g @ 400 Hz | 0.369708 | 10.0 | 10 |
| 789 | 1970.323197 | Add 2g @ 400 Hz | 0.335365 | 10.0 | 10 |
| 790 | 1980.324838 | Add 2g @ 400 Hz | 0.378497 | 10.0 | 10 |
| 791 | 1990.326478 | Add 2g @ 400 Hz | 0.346982 | 10.0 | 10 |
104548 rows × 5 columns
[ ]:
fig = px.line(
ffts,
x='frequency (Hz)',
y='value',
color='variable',
log_y=True,
log_x=True,
facet_row='Time',
facet_col='Bin Width',
title='FFTs: Acceleration (g) vs Frequency (Hz)',
labels={'value':'',
'frequency (Hz)':'',
'variable':''}
)
fig.update_layout(width=800,height=600)
fig.show(renderer='svg')
Our peaks stay consistent around the 2g we’d expect… but what is happening with the other frequency content!?
PSDs¶
[ ]:
psd = endaq.calc.psd.welch(navmat,bin_width=1)
fig = px.line(psd[20:2000])
fig.update_layout(
title_text='NAVMAT P-9492 PSD (1 Hz Bin Width)',
yaxis_title_text='Acceleration (g^2/Hz)',
xaxis_title_text='Frequency (Hz)',
xaxis_type='log',
yaxis_type='log',
legend_title_text=''
)
Now let’s do the same comparison of PSDs
[ ]:
psds = pd.DataFrame()
for bin in bins:
for time in times:
bin_t = bin
if bin=='1/T':
bin_t = 1/time
psd = endaq.calc.psd.welch(
navmat[:time], bin_width=bin_t)
psd = psd[20:2000].reset_index().melt(id_vars='frequency (Hz)')
psd['Time'] = time
psd['Bin Width'] = bin
psds = pd.concat([psds,psd])
[ ]:
fig = px.line(
psds,
x='frequency (Hz)',
y='value',
color='variable',
log_y=True,
log_x=True,
facet_row='Time',
facet_col='Bin Width',
title='PSDs: Acceleration (g^2/Hz) vs Frequency (Hz)',
labels={'value':'',
'frequency (Hz)':'',
'variable':''}
)
fig.update_layout(width=800,height=600)
fig.show(renderer='svg')
The peak at those sine tones decrease yet the bin width was wider and that sine tone was at one single frequency… so it is less dense. But then the other random/broadband levels are consistent regardless of our length of time or frequency resolution.
PSD Frequency Resolution and Octave Spacing¶
[ ]:
psd_coarse = endaq.calc.psd.welch(navmat,bin_width=10)
fig = px.line(psd_coarse[20:2000])
fig.update_layout(
title_text='NAVMAT P-9492 PSD (10 Hz Bin Width)',
yaxis_title_text='Acceleration (g^2/Hz)',
xaxis_title_text='Frequency (Hz)',
xaxis_type='log',
yaxis_type='log',
legend_title_text=''
)
Convert to an octave spaced PSD with to_octave() docs.
[ ]:
psd = endaq.calc.psd.welch(navmat,bin_width=1)
oct_psd = endaq.calc.psd.to_octave(psd,fstart=20,octave_bins=3)
fig = px.line(oct_psd[:2000])
fig.update_layout(
title_text='NAVMAT P-9492 PSD 1/3 Octave',
yaxis_title_text='Acceleration (g^2/Hz)',
xaxis_title_text='Frequency (Hz)',
xaxis_type='log',
yaxis_type='log',
legend_title_text='',
template='endaq_light'
)
/usr/local/lib/python3.7/dist-packages/endaq/calc/psd.py:161: RuntimeWarning:
empty frequency bins in re-binned PSD; original PSD's frequency spacing is too coarse
Cumulative Sum from PSD¶
[ ]:
cum_rms = endaq.calc.psd.welch(navmat,bin_width=1, scaling='parseval').cumsum()**0.5
fig = px.line(cum_rms[10:2000])
fig.update_layout(
title_text='NAVMAT P-9492 PSD with Added Sine Tone',
yaxis_title_text='Cumulative Acceleration RMS (g)',
xaxis_title_text='Frequency (Hz)',
xaxis_type='log',
legend_title_text=''
)
Random Vibration Examples¶
Bearing¶
The first example was the topic of our blog on top 12 vibration metrics.
[ ]:
bearing = pd.read_csv('https://info.endaq.com/hubfs/Plots/bearing_data.csv', index_col=0)
[ ]:
endaq.plot.rolling_min_max_envelope(bearing, plot_as_bars=True, desired_num_points=500, opacity=0.8)
[ ]:
psd = endaq.calc.psd.welch(bearing,bin_width=10)
fig = px.line(psd)
fig.update_layout(
title_text='Bearing Vibration',
yaxis_title_text='Acceleration (g^2/Hz)',
xaxis_title_text='Frequency (Hz)',
xaxis_type='log',
yaxis_type='log',
legend_title_text='',
template='endaq_light'
)
Car Engine¶
During a morning commute (many years ago) I mounted an enDAQ sensor to the car’s engine.
[ ]:
engine = endaq.ide.to_pandas(endaq.ide.get_doc('https://info.endaq.com/hubfs/data/Commute.ide').channels[8])
engine = endaq.calc.filters.butterworth(engine,low_cutoff=1)
[ ]:
endaq.plot.rolling_min_max_envelope(engine, plot_as_bars=True, desired_num_points=500, opacity=0.8)
[ ]:
psd = endaq.calc.psd.welch(engine,bin_width=1)
fig = px.line(psd)
fig.update_layout(
title_text='VIbration of an Engine',
yaxis_title_text='Acceleration (g^2/Hz)',
xaxis_title_text='Frequency (Hz)',
xaxis_type='log',
yaxis_type='log',
legend_title_text='',
template='endaq_light'
)
Here we’ll use the octave_spectrogram() (see docs) to generate a spectrogram with log spaced frequency bins.
[ ]:
data, fig = endaq.plot.octave_spectrogram(engine[['Z']], window=2, bins_per_octave=24, freq_start= 20, max_freq=100)
fig.show()
/usr/local/lib/python3.7/dist-packages/endaq/calc/psd.py:161: RuntimeWarning:
empty frequency bins in re-binned PSD; original PSD's frequency spacing is too coarse
[ ]:
data = 10 ** (data/10)
fig = px.line(data[data.index<500].idxmax())
fig.update_layout(
title_text="Moving Peak Frequency",
xaxis_title_text="",
yaxis_title_text="Peak Frequency (Hz)",
showlegend=False
)
fig.show()
Quick Poll - What FFT Support Should We Add?¶
Remember this is an open source library you can view, comment and “react” to feature requests and bug reports. Here is an “issue” created to document this need to add some FFT support.
Simple Shock Response Spectrums¶
We’ll look at two datasets in our blog on pseudo velocity.
Punching Bag¶
[ ]:
punch = endaq.ide.to_pandas(endaq.ide.get_doc('https://info.endaq.com/hubfs/data/Punching-Bag.ide').channels[8], time_mode='seconds')
punch = punch - punch.median()
[ ]:
endaq.plot.rolling_min_max_envelope(punch, plot_as_bars=True, desired_num_points=500, opacity=0.8)
[ ]:
fig = endaq.plot.around_peak(punch, num=1000, leading_ratio=0.2)
fig.update_layout(
xaxis_title_text='',
yaxis_title_text='Acceleration (g)',
legend_title_text=''
)
First determine the frequency bins to calculate it at.
[ ]:
freqs = endaq.calc.utils.logfreqs(punch[29:30], bins_per_octave=12)
Now perform the shock response spectrum calculation for those frequencies.
[ ]:
srs_punch = endaq.calc.shock.shock_spectrum(punch[29:30], freqs=freqs, damp=0.05, mode='srs')
Now plot!
[ ]:
fig = px.line(srs_punch)
fig.update_layout(
title_text='Shock Response Spectrum (SRS) of Punching Bag',
xaxis_title_text="Natural Frequency (Hz)",
yaxis_title_text="Peak Acceleration (g)",
legend_title_text='',
xaxis_type="log",
yaxis_type="log",
)
Repeat for the PVSS.
[ ]:
pvss_punch = endaq.calc.shock.shock_spectrum(punch[29:30], freqs=freqs, damp=0.05, mode='pvss')
pvss_punch = pvss_punch*9.81*39.37 #convert to in/s
[ ]:
fig = px.line(pvss_punch)
fig.update_layout(
title_text='Psuedo Velocity Shock Spectrum (PVSS) of Punching Bag',
xaxis_title_text="Natural Frequency (Hz)",
yaxis_title_text="Psuedo Velocity (in/s)",
legend_title_text='',
xaxis_type="log",
yaxis_type="log",
)
MIL-S-901D Barge Shock¶
[ ]:
barge = pd.read_csv('https://info.endaq.com/hubfs/data/mil-s-901d-barge.csv', names=['Time (s)','Accel (g)']).set_index('Time (s)')
barge = barge - barge.median()
[ ]:
endaq.plot.rolling_min_max_envelope(barge, plot_as_bars=True, desired_num_points=500, opacity=0.8)
[ ]:
fig = endaq.plot.around_peak(barge, num=1000, leading_ratio=0.2)
fig.update_layout(
xaxis_title_text='',
yaxis_title_text='Acceleration (g)',
showlegend=False
)
First determine the frequency bins to calculate it at. Here though we will specify an initial frequency of one lower than the duration.
[ ]:
freqs = endaq.calc.utils.logfreqs(barge, init_freq=1, bins_per_octave=12)
/usr/local/lib/python3.7/dist-packages/endaq/calc/utils.py:54: RuntimeWarning:
the data's duration is too short to accurately represent an initial frequency of 1.000 Hz
Now perform the shock response spectrum calculation for those frequencies.
[ ]:
srs_barge = endaq.calc.shock.shock_spectrum(barge, freqs=freqs, damp=0.05, mode='srs')
Now plot!
[ ]:
fig = px.line(srs_barge)
fig.update_layout(
title_text='Shock Response Spectrum (SRS) of MIL-S-901 Barge',
xaxis_title_text="Natural Frequency (Hz)",
yaxis_title_text="Peak Acceleration (g)",
legend_title_text='',
xaxis_type="log",
yaxis_type="log",
)
Repeat for the PVSS.
[ ]:
pvss_barge = endaq.calc.shock.shock_spectrum(barge, freqs=freqs, damp=0.05, mode='pvss')
pvss_barge = pvss_barge*9.81*39.37 #convert to in/s
[ ]:
fig = px.line(pvss_barge)
fig.update_layout(
title_text='Psuedo Velocity Shock Spectrum (PVSS) of MIL-S-901 Barge',
xaxis_title_text="Natural Frequency (Hz)",
yaxis_title_text="Psuedo Velocity (in/s)",
legend_title_text='',
xaxis_type="log",
yaxis_type="log",
)
Compare¶
[ ]:
srs_punch = srs_punch[['Z (100g)']].reset_index().melt(id_vars='frequency (Hz)')
srs_punch['variable'] = 'Punching Bag (80g Peak)'
srs_barge = srs_barge.reset_index().melt(id_vars='frequency (Hz)')
srs_barge['variable'] = 'MIL-S-901 (600g Peak)'
srs_combined = pd.concat([srs_punch, srs_barge])
[ ]:
fig = px.line(
srs_combined,
x='frequency (Hz)',
y='value',
color='variable'
)
fig.update_layout(
title_text='Shock Response Spectrum (SRS) Comparison',
xaxis_title_text="Natural Frequency (Hz)",
yaxis_title_text="Peak Acceleration (g)",
legend_title_text='',
xaxis_type="log",
yaxis_type="log",
)
[ ]:
pvss_punch = pvss_punch[['Z (100g)']].reset_index().melt(id_vars='frequency (Hz)')
pvss_punch['variable'] = 'Punching Bag (80g Peak)'
pvss_barge = pvss_barge.reset_index().melt(id_vars='frequency (Hz)')
pvss_barge['variable'] = 'MIL-S-901 (600g Peak)'
pvss_combined = pd.concat([pvss_punch, pvss_barge])
[ ]:
fig = px.line(
pvss_combined,
x='frequency (Hz)',
y='value',
color='variable'
)
fig.update_layout(
title_text='Psuedo Velocity Shock Spectrum (PVSS) Comparison',
xaxis_title_text="Natural Frequency (Hz)",
yaxis_title_text="Psuedo Velocity (in/s)",
legend_title_text='',
xaxis_type="log",
yaxis_type="log",
)
Peak Finding¶
[ ]:
bumps = endaq.ide.to_pandas(endaq.ide.get_doc('https://info.endaq.com/hubfs/data/Robotic-Bumps.ide').channels[80], time_mode='seconds')
bumps = bumps - bumps.median()
[ ]:
fig = endaq.plot.rolling_min_max_envelope(bumps, plot_as_bars=True, desired_num_points=500, opacity=0.8)
fig.show()
Now we’ll use SciPy’s find_peaks function to isolate the major events.
[ ]:
peak_times, _ = scipy.signal.find_peaks(
x = bumps['Y (40g)'].abs(),
distance = 5 / endaq.calc.utils.sample_spacing(bumps), #spaced 5 seconds apart
height = 8
)
Let’s add them to the previous plot!
[ ]:
fig.add_trace(go.Scatter(
x=bumps.iloc[peak_times].index,
y=bumps.iloc[peak_times]['Y (40g)'],
name='Peaks',
mode='markers',
marker_size=10,
marker_color='#D72D2D'
))
fig.show()
Now let’s plot the peak event with the identified peak.
[ ]:
fig = endaq.plot.around_peak(bumps, num=1000, leading_ratio=0.2)
fig.update_layout(
xaxis_title_text='',
yaxis_title_text='Acceleration (g)',
legend_title_text=''
)
fig.add_trace(go.Scatter(
x=[bumps.iloc[peak_times[2]].name],
y=[bumps.iloc[peak_times[2]]['Y (40g)']],
name='Peak',
mode='markers',
marker_size=10,
marker_color='#D72D2D'
))
fig.show()
PVSS of Full Time History¶
[ ]:
freqs = endaq.calc.utils.logfreqs(bumps, init_freq=1, bins_per_octave=12)
pvss_bumps = endaq.calc.shock.shock_spectrum(bumps, freqs=freqs, damp=0.05, mode='pvss')
pvss_bumps = pvss_bumps*9.81*39.37 #convert to in/s
[ ]:
fig = px.line(pvss_bumps)
fig.update_layout(
title_text='Psuedo Velocity Shock Spectrum (PVSS) of Robotic "Bumps"',
xaxis_title_text="Natural Frequency (Hz)",
yaxis_title_text="Psuedo Velocity (in/s)",
legend_title_text='',
xaxis_type="log",
yaxis_type="log",
)
You may be surprised to see the X axis actually had higher peak velocities than the Y axis because of where the frequency content lies!
Loop Through All Peaks¶
[ ]:
pvss_all = pd.DataFrame()
for peak in peak_times:
freqs = endaq.calc.utils.logfreqs(bumps.iloc[peak-1000:peak+4000], init_freq=1, bins_per_octave=12)
pvss = endaq.calc.shock.shock_spectrum(bumps.iloc[peak-1000:peak+4000], freqs=freqs, damp=0.05, mode='pvss')*9.81*39.37 #convert to in/s
pvss = pvss.reset_index().melt(id_vars='frequency (Hz)')
pvss['Peak'] = np.abs(bumps.iloc[peak]['Y (40g)'])
pvss['Time'] = bumps.index[peak]
pvss_all = pd.concat([pvss_all,pvss])
[ ]:
pvss_all['Peak'] = np.round(pvss_all['Peak'],1)
fig = px.line(
pvss_all,
x='frequency (Hz)',
y='value',
facet_col='variable',
color='Peak',
hover_data=['value','Time'],
log_x=True,
log_y=True,
title='Comparison of PVSS for Each Event',
labels={'value':'Peak Pseudo Velocity (in/s)','frequency (Hz)':''}
)
fig.for_each_annotation(lambda a: a.update(text=a.text.split("=")[-1]))
fig.show()
Notice how the peak at 23.5g has a pseudo velocity about 1/2 that compared to the peak at virtually all the other events, including the one at 12.8g.
Preview of Batch¶
This is currently available, see docs, but we are working on a few bug fixes and improved functionality. This module allows you to batch process many IDE (only works for our sensors for now).
In a seperate document I first executed the following code to gather all the .IDE files I wanted to analyze (I hide the actual folder name). ~~~python import glob directory = r“C:\Users\shanly\enDAQ-Notebooks…”+“\”
files = glob.glob(directory+“.ide”) #get all the files in that directory with a .ide extension ~~~
Then with this list of files, I performed the batch operation with the following. ~[STRIKEOUT:python calc_output = ( endaq.batch.GetDataBuilder(accel_highpass_cutoff=1) .add_psd(freq_bin_width=1) .add_metrics() .aggregate_data(files) ) file_data = calc_output.dataframes]~
Then I saved the output dataframes of interest to pickles that I will load next! ~[STRIKEOUT:python file_data[‘psd’].to_pickle(‘batch_psd.pkl’, protocol=4) file_data[‘metrics’].to_pickle(‘batch_metrics.pkl’, protocol=4)]~
Note that I obscured the actual filenames (that would have contained the path) with these lines prior to saving. ~[STRIKEOUT:python file_data[‘metrics’].filename = file_data[‘metrics’].filename.str.split(‘\’).str[-1].str.split(‘.IDE’).str[0] file_data[‘psd’].filename = file_data[‘psd’].filename.str.split(‘\’).str[-1].str.split(‘.IDE’).str[0]]~
Metrics¶
[ ]:
metrics = pd.read_pickle('https://info.endaq.com/hubfs/data/batch_metrics.pkl')
metrics
| filename | calculation | axis | value | serial number | start time | |
|---|---|---|---|---|---|---|
| 0 | DAQ11409_000061 | RMS Acceleration | X (40g) | 0.050146 | 11409 | 2021-10-27 17:33:19.722259 |
| 1 | DAQ11409_000061 | RMS Velocity | X (40g) | 44.938216 | 11409 | 2021-10-27 17:33:19.722259 |
| 2 | DAQ11409_000061 | RMS Displacement | X (40g) | 5.836992 | 11409 | 2021-10-27 17:33:19.722259 |
| 3 | DAQ11409_000061 | Peak Absolute Acceleration | X (40g) | 0.906830 | 11409 | 2021-10-27 17:33:19.722259 |
| 4 | DAQ11409_000061 | Peak Pseudo Velocity Shock Spectrum | X (40g) | 0.002361 | 11409 | 2021-10-27 17:33:19.722259 |
| ... | ... | ... | ... | ... | ... | ... |
| 148258 | DAQ11409_005795 | RMS Angular Velocity | X | 1.541428 | 11409 | 2021-11-16 19:52:53.617858 |
| 148259 | DAQ11409_005795 | RMS Angular Velocity | Y | 0.344340 | 11409 | 2021-11-16 19:52:53.617858 |
| 148260 | DAQ11409_005795 | RMS Angular Velocity | Z | 0.057123 | 11409 | 2021-11-16 19:52:53.617858 |
| 148261 | DAQ11409_005795 | Average Temperature | Pressure/Temperature:00 | 15.580078 | 11409 | 2021-11-16 19:52:53.617858 |
| 148262 | DAQ11409_005795 | Average Temperature | Control Pad Pressure | 89.527103 | 11409 | 2021-11-16 19:52:53.617858 |
148263 rows × 6 columns
[ ]:
metrics.calculation.unique()
array(['RMS Acceleration', 'RMS Velocity', 'RMS Displacement',
'Peak Absolute Acceleration',
'Peak Pseudo Velocity Shock Spectrum', 'RMS Angular Velocity',
'Average Temperature'], dtype=object)
[ ]:
fig = px.scatter(
metrics[metrics.calculation.isin(['RMS Acceleration',
'RMS Displacement',
'Peak Absolute Acceleration'])],
x='start time',
y='value',
facet_col='calculation',
facet_col_wrap=1,
color='axis',
labels={'value':'',
'start time':'',
'axis':''
},
hover_data=['filename']
)
fig.update_layout(height=600)
fig.for_each_annotation(lambda a: a.update(text=a.text.split("=")[-1]))
fig.update_yaxes(matches=None)
fig.show()
PSDs¶
[ ]:
psd = pd.read_pickle('https://info.endaq.com/hubfs/data/batch_psd.pkl')
psd
| filename | axis | frequency (Hz) | value | serial number | start time | |
|---|---|---|---|---|---|---|
| 0 | DAQ11409_000061 | X (40g) | 0.000000 | 7.402487e-10 | 11409 | 2021-10-27 17:33:19.722259 |
| 1 | DAQ11409_000061 | Y (40g) | 0.000000 | 2.419061e-08 | 11409 | 2021-10-27 17:33:19.722259 |
| 2 | DAQ11409_000061 | Z (40g) | 0.000000 | 4.245836e-09 | 11409 | 2021-10-27 17:33:19.722259 |
| 3 | DAQ11409_000061 | Resultant | 0.000000 | 2.917670e-08 | 11409 | 2021-10-27 17:33:19.722259 |
| 4 | DAQ11409_000061 | X (40g) | 1.003505 | 4.808626e-09 | 11409 | 2021-10-27 17:33:19.722259 |
| ... | ... | ... | ... | ... | ... | ... |
| 2876195 | DAQ11409_005795 | Resultant | 124.448957 | 7.143454e-08 | 11409 | 2021-11-16 19:52:53.617858 |
| 2876196 | DAQ11409_005795 | X (40g) | 125.452578 | 1.768300e-08 | 11409 | 2021-11-16 19:52:53.617858 |
| 2876197 | DAQ11409_005795 | Y (40g) | 125.452578 | 3.348997e-09 | 11409 | 2021-11-16 19:52:53.617858 |
| 2876198 | DAQ11409_005795 | Z (40g) | 125.452578 | 5.949278e-08 | 11409 | 2021-11-16 19:52:53.617858 |
| 2876199 | DAQ11409_005795 | Resultant | 125.452578 | 8.052478e-08 | 11409 | 2021-11-16 19:52:53.617858 |
2876200 rows × 6 columns
Now we want to aggregate this see how things changed over time. So we’ll round the frequency values and focus on one axis. For readability we’ll also make a new column that will display time into the test in days.
[ ]:
psd['frequency (Hz)'] = np.round(psd['frequency (Hz)'] ,0)
psd['start time'] = pd.to_datetime(psd['start time'])
psd['Test Day'] = psd['start time']-psd['start time'].iloc[0]
psd['Test Day'] = np.round(psd['Test Day'].dt.total_seconds()/60/60/24,3)
psd_y = psd[psd.axis=='Y (40g)'].copy()
psd_y
| filename | axis | frequency (Hz) | value | serial number | start time | Test Day | |
|---|---|---|---|---|---|---|---|
| 1 | DAQ11409_000061 | Y (40g) | 0.0 | 2.419061e-08 | 11409 | 2021-10-27 17:33:19.722259 | 0.000 |
| 5 | DAQ11409_000061 | Y (40g) | 1.0 | 2.557175e-07 | 11409 | 2021-10-27 17:33:19.722259 | 0.000 |
| 9 | DAQ11409_000061 | Y (40g) | 2.0 | 2.522567e-06 | 11409 | 2021-10-27 17:33:19.722259 | 0.000 |
| 13 | DAQ11409_000061 | Y (40g) | 3.0 | 1.247001e-06 | 11409 | 2021-10-27 17:33:19.722259 | 0.000 |
| 17 | DAQ11409_000061 | Y (40g) | 4.0 | 7.596711e-08 | 11409 | 2021-10-27 17:33:19.722259 | 0.000 |
| ... | ... | ... | ... | ... | ... | ... | ... |
| 2876181 | DAQ11409_005795 | Y (40g) | 121.0 | 1.037411e-08 | 11409 | 2021-11-16 19:52:53.617858 | 20.097 |
| 2876185 | DAQ11409_005795 | Y (40g) | 122.0 | 6.082880e-09 | 11409 | 2021-11-16 19:52:53.617858 | 20.097 |
| 2876189 | DAQ11409_005795 | Y (40g) | 123.0 | 5.461760e-09 | 11409 | 2021-11-16 19:52:53.617858 | 20.097 |
| 2876193 | DAQ11409_005795 | Y (40g) | 124.0 | 4.885745e-09 | 11409 | 2021-11-16 19:52:53.617858 | 20.097 |
| 2876197 | DAQ11409_005795 | Y (40g) | 125.0 | 3.348997e-09 | 11409 | 2021-11-16 19:52:53.617858 | 20.097 |
719050 rows × 7 columns
2D Waterfall¶
Let’s see how the PSD changes over time in a 2D plot with a bunch of lines (one per time). To help with the visualization we first need to get a bunch of colors to map to.
[ ]:
from plotly import colors
num_colors = len(psd_y[psd_y['Test Day']<1]['Test Day'].unique())
color_steps = colors.sample_colorscale(px.colors.sequential.Turbo, num_colors)
Now we can make the plot!
[ ]:
fig = px.line(
psd_y[psd_y['Test Day']<1],
x='frequency (Hz)',
y='value',
color='Test Day',
hover_data=['filename','start time'],
color_discrete_sequence = color_steps
)
fig.update_layout(
xaxis_title_text='Frequency (Hz)',
yaxis_title_text='Acceleration (g^2/Hz)',
legend_title_text='',
legend_y=-0.7,
height=800,
xaxis_type='log',
yaxis_type='log',
template='endaq_light'
)
3D Waterfall¶
I know everyone wants to see the 3D view…
[ ]:
fig = px.line_3d(
psd_y[psd_y['Test Day']<1],
x='frequency (Hz)',
z='value',
y='Test Day',
color='Test Day',
hover_data=['filename','start time'],
color_discrete_sequence = color_steps,
log_x=True,
log_z=True,
labels={'value':'Acceleration (g^2/Hz)','frequency (Hz)':'Frequency (Hz)'}
)
fig.update_layout(
title_text='3D Waterfall Plot',
showlegend = False,
margin=dict(l=20, r=20, t=20, b=20),
template='endaq_light'
)
[ ]:
fig.write_html('3d-waterfall.html',include_plotlyjs='cdn')
Animation¶
This let’s us create animations which I’ll first do on the first day’s worth of data.
[ ]:
fig = px.line(
psd_y[psd_y['Test Day']<1],
x='frequency (Hz)',
y='value',
animation_frame='Test Day',
hover_data=['filename','start time']
)
fig.update_layout(
xaxis_title_text='Frequency (Hz)',
yaxis_title_text='Acceleration (g^2/Hz)',
legend_title_text='',
xaxis_type='log',
yaxis_type='log',
)
That’s pretty cool! But we’ll notice that the animation moves outside the inital bounds pretty quickly. So let’s first find an easy way to calculate these metrics of max/min/median per frequency bin.
[ ]:
psd_pivot = psd_y.pivot(index='frequency (Hz)', columns='start time', values='value')
psd_pivot
| start time | 2021-10-27 17:33:19.722259 | 2021-10-27 17:38:21.101715 | 2021-10-27 17:43:22.482452 | 2021-10-27 17:48:23.870605 | 2021-10-27 17:53:25.254699 | 2021-10-27 17:58:26.638977 | 2021-10-27 18:03:28.009857 | 2021-10-27 18:08:29.389068 | 2021-10-27 18:13:30.775756 | 2021-10-27 18:18:32.146697 | 2021-10-27 18:23:33.514129 | 2021-10-27 18:28:34.893768 | 2021-10-27 18:33:36.268646 | 2021-10-27 18:38:37.657501 | 2021-10-27 18:43:39.036804 | 2021-10-27 18:48:40.431610 | 2021-10-27 18:53:41.812469 | 2021-10-27 18:58:43.190490 | 2021-10-27 19:03:44.574890 | 2021-10-27 19:08:45.954772 | 2021-10-27 19:13:47.342895 | 2021-10-27 19:18:48.719848 | 2021-10-27 19:23:50.096343 | 2021-10-27 19:28:51.476501 | 2021-10-27 19:33:52.856201 | 2021-10-27 19:38:54.239196 | 2021-10-27 19:43:55.622436 | 2021-10-27 19:48:57.017181 | 2021-10-27 19:53:58.401855 | 2021-10-27 19:58:59.786193 | 2021-10-27 20:04:01.182495 | 2021-10-27 20:09:02.573852 | 2021-10-27 20:14:03.964660 | 2021-10-27 20:19:05.560089 | 2021-10-27 20:24:06.949493 | 2021-10-27 20:29:08.341552 | 2021-10-27 20:34:09.737091 | 2021-10-27 20:39:11.129425 | 2021-10-27 20:44:12.713470 | 2021-10-27 20:49:14.100280 | ... | 2021-11-16 16:35:08.246185 | 2021-11-16 16:40:12.454956 | 2021-11-16 16:45:16.662902 | 2021-11-16 16:50:20.865539 | 2021-11-16 16:55:25.078521 | 2021-11-16 17:00:29.311737 | 2021-11-16 17:05:33.518707 | 2021-11-16 17:10:37.732543 | 2021-11-16 17:15:41.967681 | 2021-11-16 17:20:46.173339 | 2021-11-16 17:25:50.585174 | 2021-11-16 17:30:54.814361 | 2021-11-16 17:35:59.042205 | 2021-11-16 17:41:03.259735 | 2021-11-16 17:46:07.486053 | 2021-11-16 17:51:11.697174 | 2021-11-16 17:56:15.934448 | 2021-11-16 18:01:20.156829 | 2021-11-16 18:06:24.380767 | 2021-11-16 18:11:28.603668 | 2021-11-16 18:16:32.835784 | 2021-11-16 18:21:37.054992 | 2021-11-16 18:26:41.778625 | 2021-11-16 18:31:45.985595 | 2021-11-16 18:36:50.203430 | 2021-11-16 18:41:54.423553 | 2021-11-16 18:46:58.631286 | 2021-11-16 18:52:02.839935 | 2021-11-16 18:57:07.076232 | 2021-11-16 19:02:11.296142 | 2021-11-16 19:07:15.528411 | 2021-11-16 19:12:19.742004 | 2021-11-16 19:17:23.986328 | 2021-11-16 19:22:28.219085 | 2021-11-16 19:27:32.438873 | 2021-11-16 19:32:36.662109 | 2021-11-16 19:37:40.912109 | 2021-11-16 19:42:45.152252 | 2021-11-16 19:47:49.379699 | 2021-11-16 19:52:53.617858 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| frequency (Hz) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 0.0 | 2.419061e-08 | 6.961451e-09 | 2.694621e-08 | 0.000004 | 0.000008 | 0.000003 | 0.000003 | 0.000003 | 0.000001 | 0.000002 | 0.000004 | 0.000005 | 0.000008 | 0.000003 | 0.000002 | 0.000003 | 0.000002 | 0.000002 | 0.000005 | 0.000002 | 0.000001 | 0.000003 | 9.199357e-07 | 0.000003 | 1.518771e-06 | 0.000002 | 0.000002 | 2.163578e-06 | 0.000008 | 0.000002 | 0.000004 | 3.760117e-06 | 8.331635e-07 | 0.000002 | 2.212025e-06 | 1.235489e-06 | 2.958984e-06 | 1.301514e-06 | 1.982634e-06 | 0.000005 | ... | 0.000003 | 3.022666e-06 | 4.218103e-06 | 0.000008 | 3.078788e-06 | 0.000002 | 2.032640e-06 | 7.642987e-06 | 2.100572e-06 | 3.379650e-06 | 2.492302e-06 | 9.384487e-06 | 2.791448e-06 | 2.543345e-06 | 0.000002 | 2.078568e-06 | 8.132484e-07 | 2.838021e-06 | 0.000004 | 4.413651e-06 | 0.000002 | 6.958460e-06 | 0.000005 | 2.259085e-06 | 2.582262e-06 | 8.285179e-06 | 0.000004 | 7.115846e-06 | 1.923488e-06 | 1.178528e-06 | 0.000005 | 1.850663e-07 | 5.758527e-08 | 4.356333e-08 | 1.326678e-08 | 3.523284e-08 | 3.401198e-08 | 9.321506e-08 | 2.072132e-07 | 5.329716e-08 |
| 1.0 | 2.557175e-07 | 8.999609e-08 | 1.926265e-07 | 0.000034 | 0.000055 | 0.000041 | 0.000037 | 0.000020 | 0.000022 | 0.000016 | 0.000045 | 0.000052 | 0.000049 | 0.000039 | 0.000026 | 0.000032 | 0.000011 | 0.000027 | 0.000051 | 0.000038 | 0.000007 | 0.000015 | 1.105532e-05 | 0.000036 | 1.671067e-05 | 0.000023 | 0.000026 | 1.953543e-05 | 0.000087 | 0.000031 | 0.000041 | 4.049195e-05 | 1.907499e-05 | 0.000032 | 2.385972e-05 | 1.026427e-05 | 2.749858e-05 | 1.615311e-05 | 2.693152e-05 | 0.000080 | ... | 0.000057 | 2.867848e-05 | 5.494686e-05 | 0.000059 | 1.791955e-05 | 0.000025 | 3.726021e-05 | 7.125737e-05 | 2.376242e-05 | 3.463165e-05 | 2.879028e-05 | 4.655712e-05 | 7.107180e-05 | 4.406466e-05 | 0.000065 | 4.128956e-05 | 1.860609e-05 | 4.077474e-05 | 0.000033 | 8.258510e-05 | 0.000014 | 7.395578e-05 | 0.000057 | 2.943697e-05 | 3.235613e-05 | 1.141953e-04 | 0.000103 | 5.089320e-05 | 3.296615e-05 | 2.210161e-05 | 0.000058 | 1.788990e-06 | 6.666895e-07 | 4.819046e-07 | 6.939725e-07 | 3.583268e-07 | 8.923644e-07 | 1.693514e-06 | 5.189828e-06 | 3.352921e-07 |
| 2.0 | 2.522567e-06 | 6.889837e-07 | 2.332143e-06 | 0.000208 | 0.000298 | 0.000202 | 0.000104 | 0.000118 | 0.000102 | 0.000077 | 0.000193 | 0.000266 | 0.000251 | 0.000146 | 0.000130 | 0.000145 | 0.000073 | 0.000150 | 0.000230 | 0.000155 | 0.000044 | 0.000097 | 4.346807e-05 | 0.000199 | 6.920640e-05 | 0.000099 | 0.000104 | 9.560500e-05 | 0.000549 | 0.000116 | 0.000247 | 3.122200e-04 | 1.225986e-04 | 0.000119 | 1.170403e-04 | 4.953305e-05 | 1.380503e-04 | 1.002347e-04 | 1.661748e-04 | 0.000339 | ... | 0.000234 | 1.086385e-04 | 3.531844e-04 | 0.000271 | 1.440112e-04 | 0.000148 | 2.247540e-04 | 3.794856e-04 | 1.091585e-04 | 1.625495e-04 | 2.139703e-04 | 2.784456e-04 | 3.102676e-04 | 2.197761e-04 | 0.000248 | 2.685322e-04 | 7.470985e-05 | 2.238129e-04 | 0.000208 | 5.037352e-04 | 0.000094 | 5.531540e-04 | 0.000472 | 1.668488e-04 | 1.696425e-04 | 5.673354e-04 | 0.000513 | 3.158666e-04 | 1.340000e-04 | 1.496420e-04 | 0.000383 | 1.414038e-05 | 4.116737e-06 | 3.061537e-06 | 3.137081e-06 | 2.238157e-06 | 3.732002e-06 | 8.260310e-06 | 2.382195e-05 | 3.364408e-06 |
| 3.0 | 1.247001e-06 | 3.708911e-07 | 1.238390e-06 | 0.000122 | 0.000155 | 0.000151 | 0.000053 | 0.000066 | 0.000059 | 0.000041 | 0.000116 | 0.000133 | 0.000148 | 0.000081 | 0.000059 | 0.000073 | 0.000037 | 0.000056 | 0.000124 | 0.000073 | 0.000026 | 0.000069 | 3.026884e-05 | 0.000104 | 4.267918e-05 | 0.000057 | 0.000043 | 6.355741e-05 | 0.000216 | 0.000054 | 0.000132 | 1.861895e-04 | 6.389375e-05 | 0.000079 | 7.598246e-05 | 4.548199e-05 | 6.775841e-05 | 6.932025e-05 | 8.357926e-05 | 0.000180 | ... | 0.000137 | 6.661549e-05 | 2.033306e-04 | 0.000178 | 1.262726e-04 | 0.000082 | 1.100094e-04 | 1.730692e-04 | 5.929123e-05 | 1.030920e-04 | 1.313220e-04 | 2.379084e-04 | 1.730239e-04 | 1.114687e-04 | 0.000104 | 1.285181e-04 | 3.582072e-05 | 1.165774e-04 | 0.000116 | 1.988762e-04 | 0.000067 | 2.372616e-04 | 0.000252 | 1.024006e-04 | 1.111846e-04 | 2.714036e-04 | 0.000222 | 2.389278e-04 | 9.763413e-05 | 8.946194e-05 | 0.000149 | 8.732022e-06 | 2.575371e-06 | 1.443267e-06 | 1.056115e-06 | 1.322230e-06 | 2.146535e-06 | 4.270818e-06 | 1.430278e-05 | 2.720061e-06 |
| 4.0 | 7.596711e-08 | 3.332906e-08 | 2.693014e-07 | 0.000026 | 0.000026 | 0.000032 | 0.000023 | 0.000020 | 0.000027 | 0.000012 | 0.000033 | 0.000023 | 0.000034 | 0.000020 | 0.000014 | 0.000018 | 0.000009 | 0.000019 | 0.000036 | 0.000024 | 0.000008 | 0.000022 | 9.036514e-06 | 0.000025 | 1.038904e-05 | 0.000017 | 0.000013 | 1.145624e-05 | 0.000039 | 0.000013 | 0.000038 | 3.526670e-05 | 1.801536e-05 | 0.000019 | 1.389114e-05 | 6.302247e-06 | 2.129335e-05 | 1.779139e-05 | 1.426981e-05 | 0.000043 | ... | 0.000059 | 1.420008e-05 | 2.916908e-05 | 0.000033 | 1.532318e-05 | 0.000016 | 1.920946e-05 | 5.402916e-05 | 1.619829e-05 | 4.107995e-05 | 2.308721e-05 | 6.647677e-05 | 5.163262e-05 | 2.292783e-05 | 0.000037 | 3.134771e-05 | 8.408034e-06 | 2.837890e-05 | 0.000028 | 4.000348e-05 | 0.000018 | 5.138282e-05 | 0.000051 | 2.366792e-05 | 2.534139e-05 | 7.182962e-05 | 0.000081 | 5.186834e-05 | 2.924370e-05 | 2.360597e-05 | 0.000056 | 1.866866e-06 | 1.077818e-06 | 6.921128e-07 | 2.991976e-07 | 1.100801e-07 | 4.083279e-07 | 3.597081e-07 | 1.828241e-06 | 4.625317e-07 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 122.0 | 4.794718e-08 | 1.403580e-09 | 1.555955e-09 | 0.000002 | 0.000013 | 0.000017 | 0.000002 | 0.000003 | 0.000003 | 0.000002 | 0.000002 | 0.000006 | 0.000004 | 0.000002 | 0.000004 | 0.000009 | 0.000021 | 0.000020 | 0.000019 | 0.000007 | 0.000008 | 0.000006 | 6.404928e-06 | 0.000012 | 1.515504e-05 | 0.000012 | 0.000003 | 1.431891e-05 | 0.000008 | 0.000004 | 0.000003 | 2.263224e-06 | 1.028560e-05 | 0.000002 | 4.241913e-06 | 4.873168e-06 | 1.225941e-06 | 3.019433e-06 | 1.951890e-06 | 0.000002 | ... | 0.000012 | 2.195231e-05 | 2.106803e-05 | 0.000012 | 1.830445e-05 | 0.000010 | 1.882487e-05 | 2.267166e-05 | 5.221777e-06 | 2.167978e-05 | 1.289279e-05 | 1.664051e-05 | 1.671418e-05 | 5.891856e-06 | 0.000015 | 1.482488e-05 | 1.265719e-05 | 1.252918e-05 | 0.000015 | 2.233010e-05 | 0.000008 | 1.701158e-05 | 0.000007 | 4.759324e-06 | 1.749558e-05 | 6.335562e-06 | 0.000006 | 2.069402e-05 | 1.063007e-05 | 7.831063e-06 | 0.000011 | 6.039101e-09 | 4.662815e-09 | 3.121494e-09 | 5.535294e-09 | 9.558629e-09 | 5.412999e-09 | 1.458804e-08 | 1.983171e-08 | 6.082880e-09 |
| 123.0 | 1.851752e-08 | 1.599072e-09 | 2.228003e-09 | 0.000002 | 0.000003 | 0.000003 | 0.000002 | 0.000002 | 0.000001 | 0.000001 | 0.000002 | 0.000002 | 0.000002 | 0.000001 | 0.000001 | 0.000003 | 0.000002 | 0.000003 | 0.000003 | 0.000001 | 0.000001 | 0.000003 | 2.084756e-06 | 0.000004 | 4.710479e-06 | 0.000002 | 0.000003 | 6.170386e-06 | 0.000003 | 0.000002 | 0.000003 | 2.033750e-06 | 2.567449e-06 | 0.000002 | 1.504151e-06 | 1.682195e-06 | 1.000708e-06 | 1.408385e-06 | 1.328178e-06 | 0.000002 | ... | 0.000003 | 4.974716e-06 | 4.804490e-06 | 0.000006 | 4.564517e-06 | 0.000003 | 4.870139e-06 | 8.099777e-06 | 2.389564e-06 | 4.807188e-06 | 2.969390e-06 | 4.548254e-06 | 5.288451e-06 | 2.222343e-06 | 0.000004 | 3.728426e-06 | 3.989563e-06 | 4.845033e-06 | 0.000005 | 6.873294e-06 | 0.000002 | 5.049589e-06 | 0.000005 | 2.686271e-06 | 5.196398e-06 | 4.537091e-06 | 0.000005 | 6.886131e-06 | 3.704323e-06 | 2.606997e-06 | 0.000003 | 5.848638e-09 | 2.652969e-09 | 3.802013e-09 | 3.680023e-09 | 7.588366e-09 | 3.352630e-09 | 1.334295e-08 | 1.356523e-08 | 5.461760e-09 |
| 124.0 | 1.526794e-08 | 1.904395e-09 | 3.012694e-09 | 0.000003 | 0.000002 | 0.000004 | 0.000004 | 0.000002 | 0.000001 | 0.000002 | 0.000005 | 0.000003 | 0.000002 | 0.000001 | 0.000001 | 0.000002 | 0.000001 | 0.000003 | 0.000005 | 0.000008 | 0.000001 | 0.000003 | 5.319471e-07 | 0.000002 | 7.423440e-07 | 0.000001 | 0.000002 | 1.331505e-06 | 0.000003 | 0.000001 | 0.000002 | 1.107081e-06 | 1.698859e-06 | 0.000001 | 7.515144e-07 | 5.368396e-07 | 7.445584e-07 | 8.629774e-07 | 1.665465e-06 | 0.000002 | ... | 0.000003 | 1.273982e-06 | 1.744378e-06 | 0.000003 | 2.006455e-06 | 0.000001 | 1.867671e-06 | 3.270818e-06 | 1.444862e-06 | 1.950836e-06 | 1.375152e-06 | 3.053077e-06 | 3.156415e-06 | 1.976571e-06 | 0.000003 | 1.392365e-06 | 9.572028e-07 | 1.487826e-06 | 0.000003 | 2.841553e-06 | 0.000002 | 2.921201e-06 | 0.000005 | 1.717473e-06 | 3.548734e-06 | 3.188935e-06 | 0.000002 | 3.984916e-06 | 1.677965e-06 | 2.226348e-06 | 0.000003 | 6.599701e-09 | 3.184131e-09 | 4.878153e-09 | 4.554283e-09 | 4.333788e-09 | 4.143943e-09 | 6.197127e-09 | 1.149195e-08 | 4.885745e-09 |
| 125.0 | 1.554448e-08 | 2.240702e-09 | 2.165436e-09 | 0.000003 | 0.000003 | 0.000004 | 0.000003 | 0.000002 | 0.000002 | 0.000003 | NaN | 0.000009 | 0.000005 | 0.000005 | 0.000002 | 0.000006 | 0.000002 | 0.000008 | 0.000019 | 0.000008 | 0.000003 | 0.000004 | 1.340032e-06 | 0.000005 | 1.828251e-06 | 0.000002 | 0.000002 | 1.030046e-06 | 0.000003 | 0.000003 | 0.000001 | 1.376330e-06 | 1.444470e-06 | NaN | 1.055394e-06 | 3.712440e-07 | NaN | 1.261323e-06 | 9.890634e-07 | 0.000003 | ... | 0.000002 | 1.289565e-06 | 1.452126e-06 | 0.000002 | 1.357979e-06 | 0.000001 | 1.266668e-06 | 2.451592e-06 | 3.529851e-07 | 1.686731e-06 | 7.846670e-07 | 2.801990e-06 | 2.365513e-06 | 8.005016e-07 | 0.000002 | 1.181413e-06 | 1.090871e-06 | 2.218299e-06 | 0.000003 | 2.916531e-06 | 0.000001 | 2.456790e-06 | 0.000001 | 2.894886e-07 | 1.862269e-06 | 9.910348e-07 | NaN | 2.436740e-06 | 9.076316e-07 | 7.792794e-07 | 0.000002 | 4.828801e-09 | 3.057908e-09 | 2.959562e-09 | 2.461398e-09 | 5.281825e-09 | 4.169273e-09 | 6.557761e-09 | 5.647898e-09 | 3.348997e-09 |
| 126.0 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | 0.000004 | 1.284312e-06 | 0.000004 | 1.629573e-06 | 0.000002 | 0.000001 | 8.839285e-07 | 0.000002 | 0.000003 | NaN | 8.535060e-07 | 6.206068e-07 | NaN | 8.059833e-07 | 1.717251e-07 | NaN | 6.507064e-07 | 5.962763e-07 | 0.000002 | ... | NaN | 3.593515e-07 | 4.812013e-07 | 0.000001 | 3.284124e-07 | NaN | 2.777564e-07 | 6.396569e-07 | NaN | 6.206701e-07 | NaN | 6.462563e-07 | 6.047255e-07 | NaN | NaN | 3.570359e-07 | 3.670580e-07 | 6.375746e-07 | 0.000002 | 9.608136e-07 | NaN | 5.880341e-07 | NaN | NaN | 4.747024e-07 | NaN | NaN | 8.688151e-07 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
127 rows × 5703 columns
In this format computing the metric per frequency bin is pretty easy:
[ ]:
psd_pivot.max(axis=1)
frequency (Hz)
0.0 0.000018
1.0 0.000155
2.0 0.000933
3.0 0.000521
4.0 0.000139
...
122.0 0.000059
123.0 0.000016
124.0 0.000011
125.0 0.000019
126.0 0.000005
Length: 127, dtype: float64
Now we can loop through and add these lines to our animation and update it.
[ ]:
def add_line(df_stat,name,dash,color):
fig.add_trace(go.Scatter(
x=df_stat.index,
y=df_stat.values,
name=name,
line_width=3,
line_dash=dash,
line_color=color
))
#Add max, min, median
for stat,dash,quant in zip(['Max','Min','Median'],
[None,None,'dash'],
[1.0,0.0,0.5]):
df_stat = psd_pivot.quantile(quant, axis=1)
add_line(df_stat,stat,dash,'#6914F0')
[ ]:
fig.update_layout(
legend_y=-0.7
)
fig.show()
That’s a Wrap!¶
Hopefully you have enough to get started but if not remember we do offer services! And we will be working on more and more documentation and examples!
[ ]: